Matthew Lombard, Temple
University, Philadelphia, PA, USA
Jennifer Snyder-Duch,
Carlow College, Pittsburgh, PA, USA
Cheryl Campanella Bracken,
Cleveland State University, Cleveland, OH, USA
Last updated on June 1, 2010
NOTES:
This document is, by design, always a work in progress. If you have information you believe should be added or updated, please e-mail the authors.
The authors have attempted to avoid violations of copyright and inappropriate use of and references to materials; if you identify a violation or related problem, please notify the authors.
Links to locations outside this document will open in a new browser window.
Quick links:
Why should content analysis researchers care about intercoder reliability?
How should content analysis researchers properly assess and report intercoder reliability?
Which measure(s) of intercoder reliability should researchers use?
How should researchers calculate intercoder reliability? What software is available?
How should content analysts set up their reliability data for use with reliability software?
How does each software tool for intercoder reliability work?
What other issues and potential problems should content analysts know about?
Where can content analysts find more information about intercoder reliability?
1. What is this site about, who created it, and why? [TOP]
In Lombard, Snyder-Duch, and Bracken (2002), we reviewed the literature regarding intercoder reliability in content analysis research and reported a study that characterized the assessment and reporting of reliability in 200 studies in the mass communication literature between 1994 and 1998. Consistent with earlier examinations (Pasadeos, Huhman, Standley, & Wilson, 1995; Riffe & Freitag, 1997), we found that only 69% (n = 137) of the articles contained any report of intercoder reliability; even in these articles, few details were provided in the average 4.5 sentences devoted to reliability and important information was ambiguously reported, not reported, or represented inappropriate decisions by researchers. Based on the literature review and these results, we proposed guidelines regarding appropriate procedures for assessment and reporting of this important aspect of content analysis.
This supplemental online resource contains:
The online format will allow us to update the information as the tools, and perspectives on the different indices and their proper use, evolve.
2. What is intercoder reliability? [TOP]
Intercoder reliability is the widely used term for the extent to which independent coders evaluate a characteristic of a message or artifact and reach the same conclusion. Although in its generic use as an indication of measurement consistency this term is appropriate and is used here, Tinsley and Weiss (1975, 2000) note that the more specific term for the type of consistency required in content analysis is intercoder (or interrater) agreement. They write that while reliability could be based on correlational (or analysis of variance) indices that assess the degree to which "ratings of different judges are the same when expressed as deviations from their means," intercoder agreement is needed in content analysis because it measures only "the extent to which the different judges tend to assign exactly the same rating to each object" (Tinsley & Weiss, 2000, p. 98); even when intercoder agreement is used for variables at the interval or ratio levels of measurement, actual agreement on the coded values (even if similar rather than identical values 'count') is the basis for assessment.
3. Why should content analysis researchers care about intercoder reliability? [TOP]
It is widely acknowledged that intercoder reliability is a critical component of content analysis, and that although it does not insure validity, when it is not established properly, the data and interpretations of the data can not be considered valid. As Neuendorf (2002) notes, "given that a goal of content analysis is to identify and record relatively objective (or at least intersubjective) characteristics of messages, reliability is paramount. Without the establishment of reliability, content analysis measures are useless" (p. 141). Kolbe and Burnett (1991) write that "interjudge reliability is often perceived as the standard measure of research quality. High levels of disagreement among judges suggest weaknesses in research methods, including the possibility of poor operational definitions, categories, and judge training" (p. 248).
A distinction is often made between the coding of manifest content, information "on the surface," and latent content under these surface elements. Potter and Levine-Donnerstein (1997) note that for latent content the coders must provide subjective interpretations based on their own mental schema and that this "only increases the importance of making the case that the judgments of coders are intersubjective, that is, those judgments, while subjectively derived, are shared across coders, and the meaning therefore is also likely to reach out to readers of the research" (p. 266).
There are important practical reasons to establish intercoder reliability too. Neuendorf (2002) argues that in addition to being a necessary, although not sufficient, step in validating a coding scheme, establishing a high level of reliability also has the practical benefit of allowing the researcher to divide the coding work among many different coders. Rust and Cooil (1994) note that intercoder reliability is important to marketing researchers in part because "high reliability makes it less likely that bad managerial decisions will result from using the data" (p. 11); Potter and Levine-Donnerstein (1997) make a similar argument regarding applied work in public information campaigns.
The bottom line is that content analysis researchers should care about intercoder reliability because not only can its proper assessment make coding more efficient, without it all of their work - data gathering, analysis, and interpretation - is likely to be dismissed by skeptical reviewers and critics.
4. How should content analysis researchers properly assess and report intercoder reliability? [TOP]
The following guidelines for the calculation and reporting of intercoder reliability are based on a review of literature concerning reliability and a detailed examination of reports of content analyses in communication journals; the literature review and study are presented in detail in Lombard, Snyder-Duch, and Bracken (2002) and Lombard, Snyder-Duch, and Bracken (2003).
First and most important, calculate and report intercoder reliability. All content analysis projects should be designed to include multiple coders of the content and the assessment and reporting of intercoder reliability among them. Reliability is a necessary (although not sufficient) criterion for validity in the study and without it all results and conclusions in the research project may justifiably be doubted or even considered meaningless.
Follow these steps in order.
1. Select one or more appropriate indices. Choose one or more appropriate indices of intercoder reliability based on the characteristics of the variables, including their level(s) of measurement, expected distributions across coding categories, and the number of coders. If percent agreement is selected (and this is not recommended), use a second index that accounts for agreement expected by chance. Be prepared to justify and explain the selection of the index or indices. Note that the selection of index or indices must precede data collection and evaluation of intercoder reliability.
2. Obtain the necessary tools to calculate the index or indices selected. Some of the indices can be calculated "by hand" (although this may be quite tedious) while others require automated calculation. A small number of specialized software applications as well as macros for established statistical software packages are available (see How should researchers calculate intercoder reliability? What software is available? below).
3. Select an appropriate minimum acceptable level of reliability for the index or indices to be used. Coefficients of .90 or greater are nearly always acceptable, .80 or greater is acceptable in most situations, and .70 may be appropriate in some exploratory studies for some indices. Higher criteria should be used for indices known to be liberal (i.e., percent agreement) and lower criteria can be used for indices known to be more conservative (Cohen's kappa, Scott's pi, and Krippendorff's alpha). A preferred approach is to calculate and report two (or more) indices, establishing a decision rule that takes into account the assumptions and/or weaknesses of each (e.g., to be considered reliable, a variable may be at or above a moderate level for a conservative index, or at or above a high level for a liberal index). In any case the researcher should be prepared to justify the criterion or criteria used.
4. Assess reliability informally during coder training. Following instrument design and preliminary coder training, assess reliability informally with a small number of units which ideally are not part of the full sample (or census) of units to be coded, and refine the instrument and coding instructions until the informal assessment suggests an adequate level of agreement.
5. Assess reliability formally in a pilot test. Using a random or other justifiable procedure, select a representative sample of units for a pilot test of intercoder reliability. The size of this sample can vary depending on the project but a good rule of thumb is 30 units (for more guidance see Lacy and Riffe, 1996). If at all possible, when selecting the original sample for the study select a separate representative sample for use in coder training and pilot testing of reliability. Coding must be done independently and without consultation or guidance; if possible, the researcher should not be a coder. If reliability levels in the pilot test are adequate, proceed to the full sample; if they are not adequate, conduct additional training, refine the coding instrument and procedures, and only in extreme cases, replace one or more coders.
6. Assess reliability formally during coding of the full sample. When confident that reliability levels will be adequate (based on the results of the pilot test of reliability), use another representative sample to assess reliability for the full sample to be coded (the reliability levels obtained in this test are the ones to be presented in all reports of the project). This sample must also be selected using a random or other justifiable procedure. The appropriate size of the sample depends on may factors but it should not be less than 50 units or 10% of the full sample, and it rarely will need to be greater than 300 units; larger reliability samples are required when the full sample is large and/or when the expected reliability level is low (Neuendorf, 2002; see Lacy and Riffe, 1996 for a discussion). The units from the pilot test of reliability can be included in this reliability sample only if the reliability levels obtained in the pilot test were adequate. As with the pilot test, this coding must be done independently, without consultation or guidance.
7. Select and follow an appropriate procedure for incorporating the coding of the reliability sample into the coding of the full sample. Unless reliability is perfect, there will be coding disagreements for some units in the reliability sample. Although an adequate level of intercoder agreement suggests that the decisions of each of the coders could reasonably be included in the final data, and although it can only address the subset of potential coder disagreements that are discovered in the process of assessing reliability, the researcher must decide how to handle these coding disagreements. Depending on the characteristics of the data and the coders, the disagreements can be resolved by randomly selecting the decisions of the different coders, using a 'majority' decision rule (when there are an odd number of coders), having the researcher or other expert serve as tie-breaker, or discussing and resolving the disagreements. The researcher should be able to justify whichever procedure is selected.
8. Report intercoder reliability in a careful, clear, and detailed manner in all research reports. Even if the assessment of intercoder reliability is adequate, readers can only evaluate a study based on the information provided, which must be both complete and clear. Provide this minimum information:
The size of and the method used to create the reliability sample, along with a justification of that method.
The relationship of the reliability sample to the full sample (i.e., whether the reliability sample is the same as the full sample, a subset of the full sample, or a separate sample).
The number of reliability coders (which must be 2 or more) and whether or not they include the researcher(s).
The amount of coding conducted by each reliability, and non-reliability, coder.
The index or indices selected to calculate reliability, and a justification of this/these selections.
The intercoder reliability level for each variable, for each index selected.
The approximate amount of training (in hours) required to reach the reliability levels reported.
How disagreements in the reliability coding were resolved in the full sample.
Where and how the reader can obtain detailed information regarding the coding instrument, procedures, and instructions (e.g., from the authors).
Do NOT use only percent agreement to calculate reliability. Despite its simplicity and widespread use, there is consensus in the methodological literature that percent agreement is a misleading and inappropriately liberal measure of intercoder agreement (at least for nominal-level variables); if it is reported at all the researcher must justify its value in the context of the attributes of the data and analyses at hand.
Do NOT use Cronbach's alpha, Pearson's r, or other correlation-based indices that standardize coder values and only measure covariation. While these indices may be used as a measure of reliability in other contexts, reliability in content analysis requires an assessment of intercoder agreement (i.e., the extent to which coders make the identical coding decisions) rather than covariation.
Do NOT use chi-square to calculate reliability.
Do NOT use overall reliability across variables, rather than reliability levels for each variable, as a standard for evaluating the reliability of the instrument.
5. Which measure(s) of intercoder reliability should researchers use? [TOP]
There are literally dozens of different measures, or indices, of intercoder reliability. Popping (1988) identified 39 different "agreement indices" for coding nominal categories, which excludes several techniques for interval and ratio level data. But only a handful of techniques are widely used.
In communication the most widely used indices are:
Just some of the indices proposed, and in some cases widely used, in other fields are Perreault and Leigh's (1989) Ir measure; Tinsley and Weiss's (1975) T index; Bennett, Alpert, and Goldstein's (1954) S index; Lin's (1989) concordance coefficient; Hughes and Garrett’s (1990) approach based on Generalizability Theory, and Rust and Cooil's (1994) approach based on "Proportional Reduction in Loss" (PRL).
It would be nice if there were one universally accepted index of intercoder reliability. But despite all the effort that scholars, methodologists and statisticians have devoted to developing and testing indices, there is no consensus on a single, "best" one.
While there are several recommendations for Cohen's kappa (e.g., Dewey (1983) argued that despite its drawbacks, kappa should still be "the measure of choice") and this index appears to be commonly used in research that involves the coding of behavior (Bakeman, 2000), others (notably Krippendorff, 1978, 1987) have argued that its characteristics make it inappropriate as a measure of intercoder agreement.
Percent agreement seems to be used most widely and is intuitively appealing and simple to calculate, but the methodological literature is consistent in identifying it as a misleading measure that overestimates true intercoder agreement (at least for nominal-level variables).
Krippendorff's alpha is well regarded and very flexible (it can be used with multiple coders, accounts for different sample sizes and missing data, and can be used for ordinal, interval and ratio level variables), but it requires tedious calculations and automated (software) options have not been widely available.
There's general consensus in the literature that indices that do not account for agreement that could be expected to occur by chance (such as percent agreement and Holsti's method) are too liberal (i.e., overestimate true agreement), while those that do can be too conservative.
And there is consensus that a few indices that are sometimes used are inappropriate: Cronbach's alpha was designed to only measure internal consistency via correlation, standardizing the means and variance of data from different coders and only measuring covariation (Hughes & Garrett, 1990), and chi-square produces high values for both agreement and disagreement deviating from agreement expected by chance (the "expected values" in the chi-square formula).
Before they examine their reliability data, researchers need to select an index of intercoder reliability based on its properties and assumptions, and the properties of their data, including the level of measurement of each variable for which agreement is to be calculated and the number of coders.
Whichever index or indices is/are used, researchers need to explain why the properties and assumptions of the index or indices they select are appropriate in the context of the characteristics of the data being evaluated.
6. How should researchers calculate intercoder reliability? What software is available? [TOP]
There are four approaches available to researchers who need to calculate intercoder reliability:
By hand
The paper-and-pencil and a hand calculator approach. This can be exceedingly tedious and in many cases impractical.
Specialized software
A very small number of software applications have been created specifically to calculate one or more reliability indices. Four considered here are:
AGREE. Popping's (1984) software calculates Cohen's kappa and an index called D2, said to be appropriate for pilot studies in which "the response categories have to be developed by the coders during the assigning process. In this situation each coder may finish with a different set and number of categories." The Windows based software was available from ProGAMMA but that company went out of business in June 2003 and AGREE is now available from SciencePlusGroup. The academic version of this software costs 399 euros (approximately $460).
Krippendorff's alpha 3.12a. This Windows program (and an earlier DOS version) calculates Krippendorff's alpha; unfortunately it is a beta or test mode program and has not been distributed widely. Klaus Krippendorff (2001, 2004) has indicated that a new and more comprehensive software application is under development. Details will likely appear on Professor Krippendorff's web site.
PRAM. The Program for Reliability Assessment
with Multiple Coders software from
Skymeg Software calculates several different indices:
Percent agreement
Scott’s pi
Cohen’s kappa
Lin’s concordance correlation coefficient
Holsti’s reliability
and
Spearman's rho
Pearson correlation coefficient
The program is not currently available online;
the authors hope to release a new version with expanded functions and an
improved user-interface in the future. In the meantime, for those conducting
solely academic research copies may be available at no cost from Professor
Kimberly Neuendorf. Note that early versions of PRAM (up to at least
v. 0.4.5) were alpha releases and the authors included a warning that they
contained bugs and were not yet finished. Be sure to check the release
notes for any version and be aware of the program's limitations.
ReCal. This is an online utility developed
by Deen Freelon, a communication doctoral student at the University of
Washington in 2008. As of October 2008, it's still in testing mode but
results so far are apparently promising. The software is available, along
with documentation and instructions, at this
web page. ReCal calculates several indices for nominal level variables:
Percent agreement
Average pairwise percent agreement (for 3+ coders)
Scott's Pi
Cohen's Kappa
Fleiss' Kappa
Krippendorff's Alpha
Statistical software packages that include reliability calculations
Two general purpose statistical software applications that include reliability calculations are:
Simstat. Available from Provalis
Research, this Windows program can be used to calculate several indices:
Percent agreement
Scott's pi
Cohen's kappa
Free marginal (nominal)
Krippendorf's r-bar
Krippendorf's R (for ordinal data)
Free marginal (ordinal)
The full version of the program costs $149 but a limited version that only
allows 20 variables is available for $40; an evaluation copy of the full
software can be downloaded at no cost but only works for 30 days or 7 uses.
SPSS. The well known Statistical Package for the Social Sciences can be used to calculate Cohen's kappa.
Macros for statistical software packages
A few people have written "macros," customized programming that can be used with existing software packages to automate the calculation of intercoder reliability. All of these are free, but require some expertise to use.
Kang, Kara, Laskey, and Seaton (1993) created and published a SAS macro that calculates Krippendorff's alpha for nominal, ordinal and interval data, Cohen's kappa, Perraults's index, and Bennet's index.
Berry and Mielke (1997) created a macro (actually a FORTRAN subroutine) to calculate a "chance-corrected index of agreement ... that measures the agreement of multiple raters with a standard set of responses (which may be one of the raters)" (p. 527). The article says that the ASTAND subroutine and "an appropriate driver program" are available from Kenneth Berry (berry@lamar.colostate.edu) in the Department of Sociology at Colorado State University.
We created some (free) SPSS macros to calculate percent agreement and Krippendorff's alpha. More information on these is below.
7. How should content analysts set up their reliability data for use with reliability software? [TOP]
Each software application that can be used to calculate intercoder reliability has its own requirements regarding data formatting, but all of them fall into two basic setup formats. In the first data setup format, used in PRAM and Krippendorff's Alpha 3.12a, each row represents the coding judgments of a particular coder for a single case across all the variables and each column represents a single variable. Data in this format appears something like this:
Unit |
var1 |
var2 |
var3 | var4 | var5 | var6 | . | . |
| case1 (coder1) | ||||||||
| case1 (coder2) | ||||||||
| case2 (coder1) | ||||||||
| case2 (coder2) | ||||||||
| case3 (coder1) | ||||||||
| case3 (coder2) | ||||||||
| . | ||||||||
| . |
In the second data setup, used in Simstat and SPSS, each row represents a single case and each column represents the coding judgments of a particular coder for a particular variable. Data in this format appears something like this:
Unit |
var1coder1 |
var1coder2 |
var2coder1 | var2coder2 | var3coder1 | var3coder2 | . | . |
| case 1 | ||||||||
| case 2 | ||||||||
| case 3 | ||||||||
| case 4 | ||||||||
| case 5 | ||||||||
| case 6 | ||||||||
| . | ||||||||
| . |
It's relatively easy to transform a data file from the first format to the second (by inserting a second copy of each column and copying data from the line of one coder to the line for the other and deleting the extra lines), but the reverse operation is more tedious. Researchers are advised to select a data setup based on the program(s) they'll use to calculate reliability.
8. How does each software tool for intercoder reliability work? [TOP]
Details about by hand calculations; AGREE, Krippendorff's Alpha 3.12a, PRAM, ReCal, Simstat and SPSS software; and macros, are presented in this section.
This doesn't involve a software tool of course, but for those who choose this technique, Neuendorf (2002) includes a very useful set of examples that illustrate the step-by-step process for percent agreement, Scott's pi, Cohen's kappa and the nominal level version of Krippendorff's alpha.
A note of caution: Avoid rounding values during by hand calculations; while each such instance may not make a substantial difference in the final reliability value, the series of them can make the final value highly inaccurate.
Examples:
Click here to view examples of by hand calculations for percent agreement, Scott's pi, Cohen's kappa and Krippendorff's alpha for a nominal level variable with two values.
Click here to view examples of by hand calculations for Krippendorff's alpha for a ratio level variable with seven values.
Popping's (1984) AGREE specialty software calculates Cohen's kappa and an index called D2 (Popping, 1983).
Data input and output:
Data can be entered from the keyboard or a plain-text file in either a "data matrix" format - a single variable version of the second data setup format above - or a "data table" (pictured in the screen shot below) which is elsewhere called an agreement matrix, where the values in the cells represent the number of cases on which two coders agreed and disagreed. Output appears on screen.
Screen shot:

Issues/limitations:
The program can handle at most 90 variables as input. The maximum number of variables allowed in one analysis is 30, the maximum number of categories per analysis is 40.
Comments:
Given its cost, researchers should be sure they need the specific functions available in this basic Windows program before purchasing it.
More information:
A fairly detailed description of the program and its features can be found here, on the web site of the current publisher, the SciencePlus Grup.
Krippendorff's Alpha 3.12a is a beta version of a program Krippendorff developed to calculate his reliability index. It has not been distributed widely and no future versions are planned, but as noted above, Krippendorff is in the process of developing a new and more comprehensive program.
Data input and output:
The program uses the first data setup format above. Data can be entered from the program but it is easier to create a plain-text, comma delimited data file (most spreadsheet programs can export data in this format) and load that file. Output (the user can select terse, medium or verbose versions) is displayed onscreen and can be saved and/or printed. Click here to view instructions for the program. Click here to view program output (for the nominal level variable used in the by hand examples above).
Screen shot:
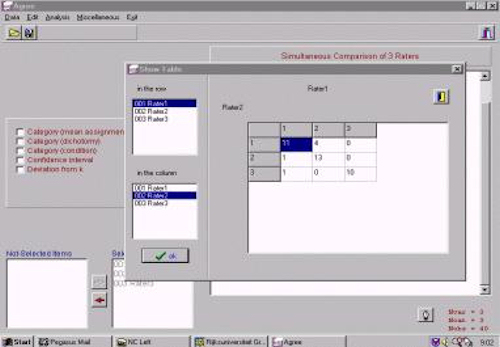
Issues/limitations:
As beta version software the program is not polished and has some limitations; a single space in the data file freezes the program, and attempting to evaluate too many variables at once can result in a very long delay followed by an error message. Krippendorff has also discovered minor (in the third decimal place) errors in some program output.
Comments:
Despite its limitations this is a useful tool for those who want to calculate the well regarded Krippendorff's alpha index. We look forward to the release of Krippendorff's new software.
More information:
See Professor Krippendorff's web site.
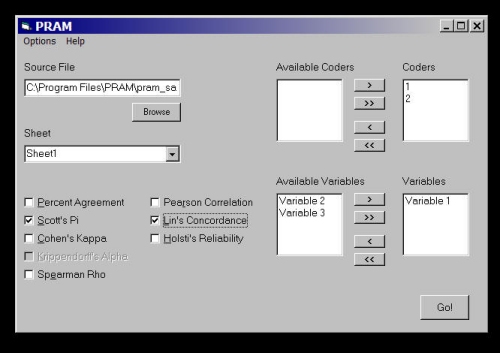
Program for Reliability Assessment with Multiple Coders (PRAM) is a new program developed in conjunction with Neuendorf's (2002) book, The content analysis guidebook. It is in alpha testing mode, and users are warned that the program still contains numerous bugs. PRAM calculates percent agreement, Scott's pi, Cohen's kappa, Lin's concordance correlation coefficient, and Holsti's reliability (as well as Spearman's rho and Pearson correlation coefficient).
Data input and output:
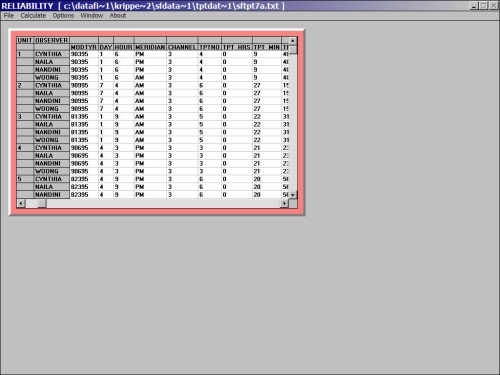
PRAM requires input in the form of a Microsoft Excel (.xls) spreadsheet file with very specific formatting. The readme.txt file notes that "The first row is a header row and must contain the variable names... The first column must contain the coder IDs in numeric form... The second column must contain the unit (case) IDs in numeric form... All other columns may contain numerically coded variables, with variable names on the header line." The program loads and evaluates the data directly from the source file - the user never sees the data matrix. The output comes in the form of another Excel file, which is automatically named pram.xls; errors are noted in a log file (pram.txt). Click here to view program output (for the nominal level variable used in the by hand examples above)
Screen shot:
Issues/limitations:
The program accommodates missing values in the form of empty cells but not special codes (e.g., "99") that represent missing values.
The data file must contain only integers (if necessary, a variable for which some or all values contain decimal points can be transformed by multiplying all values by the same multiple of 10).
The current version of the program has moderate memory limitations; the programmers recommend that data values not be greater than 100.
The programmers planned to include Krippendorff's alpha among the indices calculated but have not done so yet (the option is displayed but can't be selected).
Output for most indices includes analyses for all pairs of coders, which is a valuable diagnostic tool, but it also includes the average of these values, even for indices not designed to accommodate multiple coders; use caution in interpreting and reporting these values.
In our experience the PRAM results for Holsti's reliability are not trustworthy.
Comments:
This is an early, sometimes buggy version of what has the potential to be a very useful tool. Some calculation problems in earlier versions have apparently been solved however, as the release notes state that "All available coefficients [have been] tested and verified by Dr. [Kim] Neuendorf's students."
More information:
An online accompaniment to Neuendorf's book is available here; some limited information about PRAM is available here; more specific information about the program is in the readme.txt file that comes with it.
This online intercoder reliability calculator developed by doctoral student Deen Freelon is available, along with documentation and instructions, at this web page. It's free and calculates percent agreement, Scott's Pi, Cohen's Kappa, Fleiss' Kappa and Krippendorff's Alpha.
Data input and output:
Users create data files in the second data setup format above and upload them at the utility's web site.
Screen shot:
[forthcoming]
Issues/limitations:
[forthcoming]
Comments:
[forthcoming]
More information:
[forthcoming]
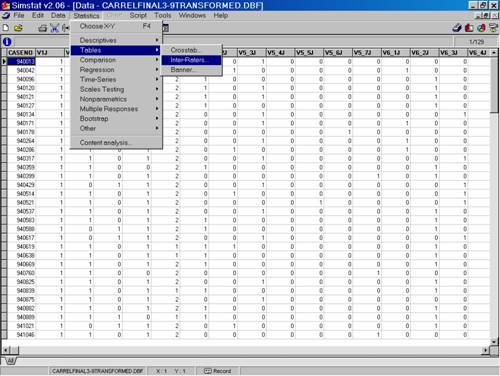
Available from Provalis Research, this Windows program calculates percent agreement, Scott's pi, Cohen's kappa, and versions of Krippendorff's alpha.
Data input and output:
The program uses the second data setup format described above. It can import data files in various formats but saves files in a proprietary format (with a .dbf file extension). To calculate reliability, the user selects "Statistics," "Tables," and then "Inter-Raters" from the menu and then selects indices and variables. The output appears in a "notebook" file on screen (and which can be printed). Click here to view program output (for the nominal level variable used in the by hand examples above).
Screen shot:
Issues/limitations:
Simstat can only evaluate the judgments of two coders.
The two versions of Krippendorff's reliability index Simstat produces are for ordinal level variables. The program's documentation states, "Krippendorf's R-bar adjustment is the ordinal extension of Scott's pi and assumes that the distributions of the categories are equal for the two sets of ratings. Krippendorf's r adjustment is the ordinal extension of Cohen's Kappa in that it adjusts for the differential tendencies of the judges in the computation of the chance factor."
In our experience Simstat occasionally has behaved erratically.
Comments:
If one already has access to this software, or cost is not an issue, this is a valuable, though limited, tool for calculating reliability.
More information:
Click here to read the program's help page regarding Inter-raters agreement statistics.
SPSS can be used to calculate Cohen's kappa.
Data input and output:
The program uses the second data setup format described above. It can import data files in various formats but saves files in a proprietary format (with a .sav file extension). As with other SPSS operations, the user has two options available to calculate Cohen's kappa. First, she can select "Analyze," "Descriptive Statistics," and "Crosstabs..." in the menus, then click on "Statistics" to bring up a dialog screen, and click on the check box for "Kappa." The second option is to prepare a syntax file containing the commands needed to make the calculations. The syntax (which can also be automatically generated with the "paste" button and then edited for further analyses), should be:
CROSSTABS
/TABLES=var1c1 BY var1c2
/FORMAT= AVALUE TABLES
/STATISTIC=CC KAPPA
/CELLS= COUNT ROW COLUMN TOTAL .
where var1c1 and var1c2 are the sets of judgments for variable 1 for coder 1 and coder 2 respectively.
The output appears in an "output" file on screen (and which can be printed). Click here to view program output (for the nominal level variable used in the by hand examples above).
Screen shot:
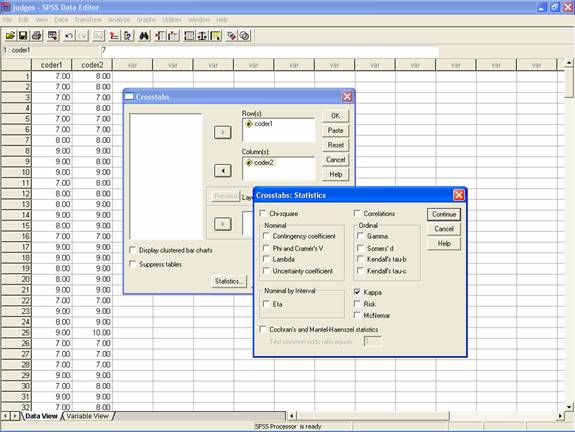
Issues/limitations:
Cohen's kappa is the only index SPSS calculates.
The program creates a symmetric (square) 2-way table of values, with the columns representing the values used by one coder and the rows representing the values used by the other coder. If in the entire dataset either coder has not used a specific value and the other coder has used that value, SPSS produces an error message ("Kappa statistics cannot be computed. They require a symmetric 2-way table in which the values of the first variable match the values of the second variable.").
Comments:
SPSS is the most established of the software that can be used to calculate reliability, but it is of limited use because it only calculates Cohen's kappa. Perhaps communication and other researchers can encourage SPSS to incorporate other indices.
More information:
The SPSS web site is http://spss.com.
Macros for statistical software packages
For researchers proficient with their use, SAS and SPSS macros to automate the calculations are available for some indices.
Data input and output:
Kang, Kara, Laskey, and Seaton (1993) created
and published a SAS macro that calculates Krippendorff's alpha for nominal,
ordinal and interval data, Cohen's kappa, Perrault's index, and Bennett's
index. The authors state:
"The calculation of intercoder agreement is essentially a two-stage
process. The first stage involves constructing an agreement matrix which
summarizes the coding results. This first stage is particularly burdensome
and is greatly facilitated by a matrix manipulation facility. Such a facility
is not commonly available in popular spreadsheet or database software,
and frequently is not available in statistical packages. The second stage
is the calculation of a specific index of intercoder agreement and is much
simpler. This second stage could be computed with any existing spreadsheet
software package... Our objective is to incorporate both sets of calculations
into a single computer run. The SAS PROC IML and MACRO facilities (in SAS
version 6 or higher) readily allow for the calculation of the agreement
matrix, very complex for multiple coders, and SAS is also capable of the
more elementary index calculations. Our SAS Macro is menu driven and is
'user friendly.'" (pp. 20-21).
The text of the macro is included in Appendix B of the article and is 3
3/4 pages long; click here for
an electronic copy that can be cut-and-pasted for use in SAS. The authors
report tests that demonstrate the validity of the macro for each of the
indices..
Berry and Mielke (1997) created a macro (actually a FORTRAN subroutine) to calculate a "chance-corrected index of agreement ... that measures the agreement of multiple raters with a standard set of responses (which may be one of the raters)" (p. 527). See the article for details.
We have created macros for use with the Windows versions
of SPSS to calculate Krippendorff's alpha and percent agreement. Instructions
for the use of the macros are included within them. A good starting point
for those interested in learning to use (and finding useful) macros for
SPSS is the Macros
page of Raynald's
SPSS Tools web site.
Krippendorff's alpha macros
Click here to
view a macro that calculates Krippendorff's alpha for one or more 2 category
nominal level variables with 2 coders, and prints details of the calculations.
Click here to
view SPSS program output for this macro for the nominal level variable
used in the by hand examples above.
Click here to view a
macro that does the same thing but does not print the detailed calculations.
Click here to view program
output for this macro for the nominal level variable used in the by hand
examples above.
These macros can be modified fairly easily for variables with different
numbers of coding categories. Click here to
view a macro that calculates Krippendorff's alpha for one or more variables
with 3 (rather than 2) nominal level coding categories, and prints details
of the calculations (or click here to
view a macro that does the same thing but does not print the detailed calculations).
A comparison of the macros for 2 and 3 category variables reveals the modifications
needed to create macros that accommodate variables with any number of coding
categories.
In principle the macros can be modified to accommodate different numbers
of coders as well (see the authors for details).
Percent agreement (not recommended)
Click here to
view a macro that calculates percent agreement for one or more nominal
level variables with 2 coders and prints details of the calculations.
Click here to
view SPSS program output for the nominal level variable used in the by
hand examples above.
Click here to view a macro
that does the same thing but does not print the detailed calculations.
Click here to view program
output for the nominal level variable used in the by hand examples above.
In May 2005 we learned of a more complete SPSS macro for Krippendorff's alpha written by Andrew F. Hayes, an Assistant Professor in the School of Communication at Ohio State University. His macro computes alpha for "any level of measurement, any number of judges, with or without missing data," and includes a bootstrapping routine that produces a 95% confidence interval for alpha and the probability that alpha is greater than a user supplied criterion. The macro is available (at no cost) at Andrew's web site (follow the "SPSS macros" link on the menu at the left and find KALPHA.SPS in the frame on the right; or use the direct link). We haven't tested it, but this looks like a great tool for content analysts. The CD that comes with Andrew's 2005 book, Statistical Methods for Communication Science, computes alpha, Scott's pi, kappa, I-sub-r, and Holsti.
Issues/limitations:
All of these macros must be used exactly as instructed to yield valid results.
Comments:
Only those familiar and comfortable with using and manipulating software are advised to use macros such as the ones described and presented here. Hopefully a usable and affordable specialized software package and/or an expanded version of a general purpose statistical software package will make the use of macros redundant and obsolete.
More information:
See the articles identified and/or contact the authors.
9. What other issues and potential problems should content analysts know about? [TOP]
Two other common considerations regarding intercoder reliability involve the number of reliability coders and the particular units (messages) they evaluate.
Many indices can be extended to three or more coders by averaging the index values for each pair of coders, but this is inappropriate because it can hide systematic, inconsistent coding decisions among the coders (on the other hand, calculations for each coder pair, which are automatically provided by some software (e.g., PRAM) can be a valuable diagnostic tool during coder training).
While most researchers have all reliability coders evaluate the same set of units, a few systematically assign judges to code overlapping sets of units. We recommend the former approach because it provides the most efficient basis for evaluating coder agreement, and along with others (e.g., Neuendorf, 2002), against the latter approach (fortunately, most indices can account for missing data that results from different coders evaluating different units, whatever the reason). See Neuendorf (2002) and Potter and Levine-Donnerstein (1999) for discussions.
10. Where can content analysts find more information about intercoder reliability? [TOP]
To supplement the information provided here the interested researcher may want to:
Review the references below
Periodically return to this online resource for updated information
11. References and bibliography [TOP]
References
Bakeman, R. (2000). Behavioral observation and coding. In H. T. Reis & C. M. Judge (Eds.), Handbook of research methods in social and personality psychology (pp. 138-159). New York: Cambridge University Press.
Bennett, E. M., Alpert, R., & Goldstein, A. C. (1954). Communications through limited response questioning. Public Opinion Quarterly, 18, 303-308.
Berry, K. J., & Mielke, P. W., Jr. (1997). Measuring the joint agreement between multiple raters and a standard. Educational and Psychological Measurement, 57(3), 527-530.
Dewey, M. E. (1983). Coefficients of agreement. British Journal of Psychiatry, 143, 487-489.
Hughes, M. A., & Garrett, D. E. (1990). Intercoder reliability estimation--Approaches in marketing: A Generalizability Theory framework for quantitative data. Journal of Marketing Research, 27 (May), 185-195.
Kang, N., Kara, A., Laskey, H. A., & Seaton, F. B. (1993). A SAS MACRO for calculating intercoder agreement in content analysis. Journal of Advertising, 23(2), 17-28.
Kolbe, R. H. & Burnett, M. S. (1991). Content-analysis research: An examination of applications with directives for improving research reliability and objectivity. Journal of Consumer Research, 18, 243-250.
Krippendorff, K. (1978). Reliability of binary attribute data. Biometrics, 34, 142-144.
Krippendorff, K. (1987). Association, agreement, and equity. Quality and Quantity, 21, 109-123.
Krippendorff, K. (2001, August 22). CONTENT [Electronic discussion list]. The posting is available here.
Krippendorff, K. (2004, October 23). CONTENT [Electronic discussion list]. The posting is available here.
Lacy, S., & Riffe, D. (1996). Sampling error and selecting intercoder reliability samples for nominal content categories: Sins of omission and commission in mass communication quantitative research. Journalism & Mass Communication Quarterly, 73, 969-973.
Lin, L. I. (1989). A concordance correlation coefficient to evaluate reproducibility. Biometrics, 45, 255-268.
Lombard, M., Snyder-Duch, J., & Bracken, C. C. (2002). Content analysis in mass communication: Assessment and reporting of intercoder reliability. Human Communication Research, 28, 587-604.
Lombard, M., Snyder-Duch, J., & Bracken, C. C. (2003). Correction. Human Communication Research, 29, 469-472.
Neuendorf, K. A. (2002). The content analysis guidebook. Thousand Oaks, CA: Sage.
Pasadeos, Y., Huhman, B., Standley, T., & Wilson, G. (1995, May). Applications of content analysis in news research: A critical examination. Paper presented to the Theory and Methodology Division at the annual conference of the Association for Education in Journalism and Mass Communication (AEJMC), Washington, D.C.
Perreault, W. D., & Leigh, L. E. (1989). Reliability of nominal data based on qualitative judgments. Journal of Marketing Research, 26 (May), 135-148.
Popping, R. (1983). Traces of agreement. On the dot-product as a coefficient of agreement. Quality & Quantity, 17, 1-18.
Popping, R. (1984). AGREE, a package for computing nominal scale agreement. Computational Statistics and Data Analysis, 2, 182-185.
Popping, R. (1988). On agreement indices for nominal data. In Willem E. Saris & Irmtraud N. Gallhofer (Eds.), Sociometric research: Volume 1, data collection and scaling (pp. 90-105). New York: St. Martin's Press.
Potter, W. J., & Levine-Donnerstein, D. (1999). Rethinking validity and reliability in content analysis. Journal of Applied Communication Research, 27(3), 258+.
ProGAMMA (2002). AGREE. Accessed on July 7, 2002 at http://www.gamma.rug.nl/.
Riffe, D., & Freitag, A. A. (1997). A content analysis of content analyses: Twenty-five years of Journalism Quarterly. Journalism & Mass Communication Quarterly, 74 (4), 873-882.
Rust, R., & Cooil, B. (1994). Reliability Measures for Qualitative Data: Theory and Implications. Journal of Marketing Research, 31 (February), 1-14.
Skymeg Software (2002). Program for Reliability Assessment with Multiple Coders (PRAM). Retrieved on July 7, 2002 from: http://www.geocities.com/skymegsoftware/pram.html
Tinsley, H. E. A. & Weiss, D. J. (1975). Interrater reliability and agreement of subjective judgements. Journal of Counseling Psychology, 22, 358-376.
Tinsley, H. E. A. & Weiss, D. J. (2000). Interrater reliability and agreement. In H. E. A. Tinsley & S. D. Brown, Eds., Handbook of Applied Multivariate Statistics and Mathematical Modeling, pp. 95-124. San Diego, CA: Academic Press.
Bibliography
Banerjee, M., Capozzoli, M., McSweeney, L., & Sinha, D. (1999). Beyond kappa: A review of interrater agreement measures. The Canadian Journal of Statistics, 27(1), 3-23.
Berelson, B. (1952). Content analysis in communication research. Glencoe, IL: Free Press.
Brennan, R. L., & Prediger, D. J. (1981). Coefficient kappa: Some uses, misuses, and alternatives. Educational and Psychological Measurement, 41, 687-699.
Cohen, J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20(1), 37-46.
Cohen, J. (1968). Weighted kappa: Nominal scale agreement with provision for scaled disagreement of partial credit. Psychological Bulletin, 70(4), 213-220.
Craig, R. T. (1981). Generalization of Scott's Index of Intercoder Agreement. Public Opinion Quarterly, 45(2), 260-264.
Ellis, L. (1994). Research methods in the social sciences. Madison, WI: WCB Brown & Benchmark.
Fleiss, J. L. (1971). Measuring nominal scale agreement among many raters. Psychological Bulletin, 76, 378-382.
Frey, L. R., Botan, C. H., & Kreps, G. L. (2000). Investigating communication: An introduction to research methods (2nd ed.). Boston, MA: Allyn and Bacon.
"Interrater Reliability" (2001). Journal of Consumer Psychology, 10(1&2), 71-73.
Holsti (1969). Content analysis for the social sciences and humanities. Reading, MA: Addison-Wesley.
Krippendorff, K. (1980). Content analysis: An introduction to its methodology. Beverly Hills, CA: Sage.
Lawlis, G. F., & Lu, E. (1972). Judgment of counseling process: Reliability, agreement, and error. Psychological Bulletin, 78, 17-20.
Lichter, S. R., Lichter, L. S., & Amundsom, D. (1997). Does Hollywood hate business or money? Journal of Communication, 47 (1), 68-84.
Riffe, D., Lacy, S., & Fico, F. G. (1998). Analyzing media messages: Using quantitative content analysis in research. Mahwah, NJ: Lawrence Erlbaum.
Scott, W. (1955). Reliability of content analysis: The case of nominal scale coding. Public Opinion Quarterly, 17, 321-325.
Seun, H. K., & Lee, P. S. C. (1985). Effects of the use of percentage agreement on behavioral observation reliabilities: A reassessment. Journal of Psychopathology and Behavioral Assessment, 7, 221-234.
Singletary, M. W. (1993). Mass communication research: Contemporary methods and applications. Addison-Wesley.